As Operações do Cálculo Diferencial e Integral:
Parte II – Acréscimo e Diferencial

 

João Cardoso Pereira Netto
(Univ. Mogi das Cruzes)

 

Introdução

É comum considerar as operações matemáticas representadas por Dx e dx como sendo de mesma natureza; contudo, embora em certas circunstâncias elas possam ser identificadas uma com a outra, em geral possuem significados diferentes. Neste artigo procura-se mostrar as propriedades de cada um desses operadores e seus significados diante dos fenômenos das Ciências Exatas.

Acréscimo e Diferencial 

Considere uma função y = f(x), contínua e definida no intervalo [a, b]. Para cada uma das variáveis x e y, pode-se escrever os seguintes operadores matemáticos:

Dx , dx       e        Dy , dy

O primeiro deles, Dx, Dy, é denominado acréscimo [1a, 2a], incremento, diferença finita, ou simplesmente diferença em x ou y, enquanto que o segundo, dx, dy, é denominado diferencial [1b, 2b, 3a, 4a]  de x, ou diferencial de y.

Diferença Finita

O símbolo Dx (ou Dy) representa uma diferença finita entre dois valores da grandeza x (ou y); consequentemente, subentende-se que ela seja mensurável fisicamente (mesmo do ponto de vista teórico). Por representar uma diferença, o símbolo D tem o significado de um incremento, acréscimo, intervalo, etc.; é definido por:

Dx = x₂ – x₁   ,   Dy = y₂ – y₁                                              (1)

onde se mostra claramente que D significa a diferença entre os valores final e inicial de uma grandeza.

As diferenças finitas são muito utilizadas na definição de grandezas físicas médias; assim, a velocidade e a aceleração médias de uma partícula, são definidas por [5]:

                                                      (2)

e                                                                                           

                                                       (3)

onde S₁, S₂, v₁ e v₂ são as posições e as velocidades da partícula nos instantes t₁ e t₂ ,e  e  indicam a velocidade e a aceleração médias. Outro exemplo da aplicação das diferenças finitas encontra-se na definição de grandezas relacionadas com a deformação dos materiais; assim, no caso da variação do comprimento L e do volume V de uma material, são definidas as grandezas [6]:

a)                  deformação de tração:

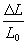
onde

DL = L - L₀

e L₀ e L são os comprimentos inicial e final do processo de deformação;

b)                  deformação volumétrica:

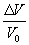
onde

DV = V - V₀

e V₀ e V são os volumes inicial e final do material no processo de deformação.

Uma característica dessa representação simbólica é que o símbolo D (delta) só deve estar associado a grandezas que sejam funções de ponto; não tem significado sua aplicação a grandezas que tenham comportamento de funções de linha, a não ser em casos particulares, uma vez que a diferença:

Dx = x₂ – x₁

significa o valor da grandeza x no estado final 2 menos o valor de x no estado inicial 1.

Em alguns casos particulares uma função de linha assume características de função de ponto e, nestas condições, ela pode (mas não deve) ser representada por uma diferença; contudo, deve-se ter sempre em mente que se trata de um caso particular e não geral. Exemplificando, a equação do Primeiro Princípio da Termodinâmica na forma integrada é [7á, 8a]:

DU = Q – W                                                             (4)

onde se mostra claramente que U, a energia interna do sistema é uma propriedade termodinâmica de estado (função de ponto), enquanto que Q e W, respectivamente, o calor e o trabalho, são propriedades da transformação (funções de linha). Para os processos em que W = 0, tem-se:

DU = Q                                                              (5)

e, nestes casos, o calor assume características de função de ponto, pois se identifica com a variação de uma função de ponto. Interpretação análoga pode ser dada para o caso das transformações adiabáticas (Q = 0), para as quais se tem:

DU  =  - W                                                            (6)

e, nestas condições, é o trabalho que assume características de função de ponto.

Diferencial

A diferencial dx pode ser definida a partir de uma condição limite sobre Dx, fazendo-a tender a zero, isto é,

          lim Dx    =  dx                                                         (7)

                D_x®0

O símbolo d é a representação matemática da diferencial, de modo que para a função y = f(x), tem-se:

dx- diferencial da variável independente x (lê-se diferencial de x ou simplesmente, “de x”)

dy = d[f(x)]- diferencial da variável dependente y ou diferencial de f(x).

A representação dx, dy significa que a diferença "x₂ – x₁", ou "y₂ – y₁" é tão pequena (um infinitésimo), que não tem mais sentido escrevê-la na forma anterior, Dx. É como se estivesse considerando o valor de uma propriedade em duas situações distintas e consecutivas. É evidente que pela sua própria construção, a diferencial só deve ser aplicada às funções contínuas; daí sua ampla utilização no Cálculo Diferencial e Integral. A diferencial também pode ser interpretada como uma diferença não mensurável (que não pode ser medida) fisicamente.

Como as funções contínuas podem ser classificadas em funções de ponto ou funções de linha, a operação diferencial aplicada a cada tipo de função conduz a resultados diferentes; devido a esse fato, as diferenciais podem ser classificados em:

a) diferencial total ou exata;

b) diferencial inexata

São apresentados em seguida as características desses dois tipos de diferenciais que têm aplicações fundamentais na Termodinâmica.

Diferencial Total ou Exata

É a aplicação da diferencial a uma função contínua que é representada por uma função de ponto [4b, 7b, 8b, 9]. Sua representação matemática é o símbolo d, já mencionado anteriormente. Toda função que possa ser representada por uma função de ponto, ou que é tomada como uma propriedade de estado, ou propriedade termodinâmica, ou ainda uma propriedade do sistema, é representada por uma diferencial exata; daí sua aplicação em praticamente todos os campos das Ciências Exatas.

Se X, Y, e Z são, individualmente, funções de ponto, as seguintes propriedades das diferenciais dessas funções são válidas:

1-  representação funcional

f (X, Y, Z)  =  0     ou     Z  =  Z(X, Y)

2- Se X = constante, então:

X = Cte,   ®   dX  =  0     ou     dX  =  0   ®   X = Cte

3- Integral entre dois estados

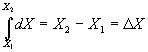
4- Inversão dos extremos

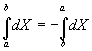
5- Integral cíclica

   ou   se    ®   X é função de ponto

6- Diferencial total ou exata

dZ  = 

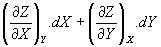
7-  Regra de Euler

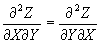
A forma de operar matematicamente a diferencial total ou exata de uma função é a mesma que as operações realizadas com as derivadas, mostrando uma certa similaridade de comportamento entre esses dois operadores; contudo, conforme será visto, eles desempenham funções bem distintas.  Uma das aplicações mais importantes das diferenciais é a seguinte: é através da variação infinitesimal das variáveis que participam de uma função que pretende representar um fenômeno, que se tornou possível obter uma relação matemática entre essas mesmas variáveis, e que irá reproduzir o comportamento do fenômeno. Esta representação chama-se equação diferencial. A etapa seguinte do procedimento matemático consiste em obter, a partir da equação diferencial, a equação que representa o comportamento do fenômeno; esta operação é realizada pelo Cálculo Integral.

Diferencial Inexata

É o Cálculo Diferencial aplicado às funções contínuas que são identificadas com as funções de linha, que na linguagem das Ciências Exatas correspondem às propriedades das transformações [7b, 8c]. É representada em geral pela letra d (não é adotado um símbolo universal para este tipo de diferencial). Se Q, R, e S são grandezas que são representadas por funções de linha, as seguintes propriedades são válidas:

1-  Representação funcional

Não existe a função f(Q, R, S) = 0; também não existe a forma S  =  S(Q, R). Esta forma funcional não pode ser escrita mesmo que contenha além das funções de linha grandezas que sejam funções de ponto.

2-  Se Q = Cte, dQ  =  0;  se dQ  =  0, então Q  =  0

3-  Integral entre dois estados

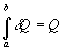
4-                  Inversão de extremos

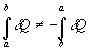
5-                  Integral cíclica

, Q é função de linha

6-                  Não tem diferencial total

7-                  Não vale a regra de Euler

A diferença de propriedades entre os dois tipos de diferenciais revela claramente a importância da distinção entre esses dois tipos de funções (ponto e linha).

Distinção entre Dx e dx

            A partir dos significados de Dx, Eq. (1) e dx, Eq. (7) de suas propriedades, é fácil notar que esses dois entes matemáticos têm significados diferentes; contudo, para dar maior clareza à essa distinção, serão ressaltados outras particularidades desses dois operadores.

            A diferença entre Df e df, onde f representa uma função qualquer não reside apenas no fato de se tratar de diferença finita e de um infinitésimo, uma vez que ocorrem também diferenças nas operações matemáticas; assim, para a função:

f(P,V) = P.V

tem-se:

D (P.V) = P₂.V₂ – P₁.V₁                                                 (8)

e

d (P.V) = P.dV + V.dP                                                 (9)

De modo análogo, para a função:

f(P, T)  = 

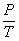
tem-se:

                                                      (10)

e

d                                     (11)

As Eq. (9) e (11) podem ser obtidas a partir das técnicas de derivação ou diferenciação. É um bom exercício observar a coerência dos termos através da análise dimensional.

Existe outra diferença importante entre Dx e dx, que é apresentada em seguida. Dx pode significar tanto o valor exato da variação de x, uma vez que a partir da forma de expressar o valor correto de uma grandeza, com seu desvio, tem-se:

Dx  =  (x₂  ±  x)  -  (x₁  ±  x)  =  x₂  -  x₁  ±  x    x

e

Dx = x₂ – x₁                                                      (1)

como o valor exato do erro cometido na medida de x. Por outro lado dx pode representar, em certas circunstâncias, um valor aproximado da medida de Dx; isto significa que para pequenos desvios da medida de x, é aceitável supor que:

Dx @ dx                                                           (12)

Esta aproximação é útil nos cálculos que envolvem funções com mais de uma variável. No caso das funções de uma variável, a relação é útil somente quando se deseja calcular o erro da medida, uma vez que o seu valor exato pode ser calculado diretamente pela Eq. (1).

Referências Bibliográficas

1-      Thomas Jr, G. B. e Finney, R. L., Cálculo Diferencial e Integral, vol. 1, Livros Técnicos e Científicos Editora S. A., R. J., 1982, a) pg. 4, b) pg. 131,

2-      Simmons, G. F., Cálculo com Geometria Analítica, vol. 1, Makron Books do Brasil Editora Ltda, S. P., 1987, a) pg. 75, b) pg. 221;

3-      Munem, A. M. e Foulis, D. J., Cálculo, vol. 1, Guanabara Dois, R. J., 1982, a) pg. 251,

4-      Kaplan, W., Cálculo Avançado, vol. 1, Editora da Universidade de São Paulo, S. P., 1972, a) pg. 20; b) pg. 93,

5-      Sears, F., Zemansky, M. W. e Young, H. D., Física, vol. 1, Livros Técnicos e científicos Editora S. A., R. J., 1985, pg. 47 a 49;

6-      Nash, W. A., Resistência dos Materiais, 2^ª ed., McGraw-Hill do Brasil Ltda, S. P., 1982, pg. 3;

7-      Atkins, P. W., Físico - Química, vol. 1, sexta edição, Livros Técnicos e Científicos Editora, R. J., 1999, a) pg. 40, b) pg. 66

8-      Castellan, G., Fundamentos de Físico - Química, Livros Técnicos e Científicos Editora, R. J., 1995, a) pg. 117; b) pg. 112, c) pg. 119,

9-      Munem, A. M. e Foulis, D. J., Cálculo, vol. 2, Guanabara Dois, R. J., 1982, pg. 866,